Counting and cardinal understanding in children with Down syndrome and typically developing children
This study compares the procedural counting ability (independently and with parental support) and conceptual understanding of cardinality of a group of children with Down syndrome and a group of typically developing children, matched for non-verbal mental age. Participants were 23 children with Down syndrome (chronological age range: 3.5 - 7 years; mental age range: 2.5 - 4 years) and 20 typically developing children (chronological age range: 2 - 4 years; mental age range: 2.5 - 4 years), and their main caregiver. The children were asked to count sets of toys (assessing procedural counting skills) and to give sets of toys (assessing understanding of cardinality), with set sizes between 2 and 18 items. The counting task was performed in two conditions, with and without parental support. The children were also asked to say the count word sequence aloud, to assess sequence production independent from object counting. The typically developing children produced significantly more number words altogether, longer standard number sequences and could count larger sets than the children with Down syndrome. Support from an adult improved performance on the count task significantly for both groups of children, and there was no significant difference between the groups in the degree of improvement, i.e. the zone of proximal development. No significant differences were found between the frequency of children (approximately one third) in each group who used counting to solve the give task, indicating an understanding of cardinality.
Nye, J, Fluck, M, and Buckley, S. (2001) Counting and cardinal understanding in children with Down syndrome and typically developing children. Down Syndrome Research and Practice, 7(2), 68-78. doi:10.3104/reports.116
Introduction
The aim of the present study was firstly to compare the performance of a group of children with Down syndrome and a group of typically developing children, matched for non-verbal mental age, on number tasks in the first phase of a longitudinal study. The number skills under investigation are production of the count word sequence, object counting, and understanding of cardinality, as measured by the ability to give a specified number of objects. Secondly, the effect of parental support for counting objects will be examined for each group.
Number skills are important prerequisites for the achievement of an independent adult lifestyle. It is surprising, therefore, that in contrast to language development, researchers have largely neglected the development of number skills in children with Down syndrome. Until recently, anecdotal reports and available research suggested that such children underachieve on number tasks compared with other skills, such as reading (Buckley, 1985; Carr, 1988; Byrne, 1997; Sloper, Turner, Cunningham, & Knussen, 1990). A more positive picture is beginning to emerge, however, as attention is drawn to increasing numbers of children and adults with Down syndrome who are successful at and enjoy mathematical activities (e.g. Caycho, Gunn, & Seigal, 1991; de Graaf & de Graaf-Posthumus, 1997; Monari-Martinez, 1998, 1999).
One of the earliest, most important number skills that children learn and use is counting. A set of five principles defining the necessary elements for a successful count was identified by Gelman and Gallistel (1978). Conflict exists over whether these are innate (Gelman & Gallistel, 1978) or acquired (Siegler & Shipley, 1987; Fuson, 1988). Gelman's first three principles, the 'how to count' principles, describe both the procedural skills required for counting and the conceptual understanding of the results. They comprise: the one-one principle - one, and only one, unique number tag must be assigned to each item counted; the stable-order principle - count words must be produced in the same order for each count; the cardinality principle - the final word of a count denotes the total number of items counted. The remaining two principles (abstraction and order-irrelevance) will not be considered here.
Gelman and Cohen (1988) found that the children with Down syndrome in their study (mental age range: 4;0 - 6;10) were, in general, not as able as "mental age matched" pre-schoolers in solving a novel counting problem, standard counting, or cardinality tests. It was concluded that typically developing children make use of innate counting principles, whereas those with Down syndrome simply learn counting procedures by rote. Closer examination reveals, however, that two of the children with Down syndrome were found to be "excellent counters" (Gelman & Cohen, 1988, p. 73) who were able to make use of principles to guide their counting. While it may be justifiable to conclude that these children are qualitatively different from the main sample, it is curious that these two individuals were ignored in drawing the final conclusion that children with Down syndrome learn to count by rote alone.
Caycho, Gunn, and Siegal (1991) replicated Gelman and Cohen's (1988) study while addressing some of its methodological problems, by matching 15 children with Down syndrome with 15 typically developing participants using receptive vocabulary. In contrast to Gelman and Cohen, they found no significant differences between the groups on tasks requiring a grasp of the counting principles. It was concluded that children with Down syndrome can make use of counting principles, and that counting competence is related to receptive language rather than to Down syndrome per se. Caycho et al. argue that the ability to employ the counting principles may be a function of the children's educational program; therefore it must not be assumed that all children will develop such understanding, just that they are capable of doing so.
Interestingly, however, Porter (1999) found that children with Down syndrome showed a different profile of development of counting skills compared with other children with learning disabilities. A larger proportion of those with Down syndrome than those with general learning disabilities, were able to successfully count a set of items themselves but were unable to detect errors made by another individual (an alternative assessement of understanding of the counting principles).
Since the current study matched children according to non-verbal general ability rather than language ability it might be expected to replicate Gelman and Cohen's (1988) finding that children with Down syndrome do not display an understanding of the counting principles (including cardinality), in contrast to matched typically developing children.
Subitization
Humans may be innately equipped to process numerical information, since it has been suggested that infants in the first year of life can distinguish between sets containing up to three or four items (Antell & Keating, 1983; Starkey, Spelke, & Gelman, 1990). This has been likened to 'subitization' in older children and adults, where the cardinal value of a small set (up to 3 or 4 items for children) is apprehended directly without overt counting (Chi & Klahr, 1975; Starkey & Cooper, 1995). There is no explicit relationship between these preverbal representations of numerosity and the verbal counting system, and children learn the appropriate number labels for subitizable sets in a piecemeal fashion, independently of counting (Wagner & Walters, 1982; Fuson, 1988; Wynn, 1992).
The only study to have investigated numerosity identification in infants with Down syndrome, found they were unable to distinguish between set sizes of two and three items, in contrast to a mental age matched group of infants with Williams syndrome, a chronological age matched group of typically developing children and a mental age matched group of typically developing children (Paterson, 2001; Paterson, Brown, Gsödle, Johnson, & Karmiloff-Smith, 1999 ). No research has investigated subitization in older children with Down syndrome, though Paterson reports results from a similar task (numerosity discrimination), with older children and adults with Down syndrome (chronological age range: 11 - 35 years) performing in a similar way to typically developing controls. For the current study, this skill has significance for interpretation of children's performance on tasks involving small sets (two and three items).
Procedural counting competence
1) One-one correspondence
The one-one principle describes how one, and only one, unique number tag must be assigned to each item counted. Gelman and Gallistel (1978) distinguish three types of errors concerning this principle: partitioning errors (double tagging or skipping items), tagging errors (giving two or more items the same tag), and coordination errors (i.e. coordination of partitioning and tagging). Gelman and Gallistel (1978) found that typically developing 2-year-olds made more partitioning errors than 3-year-olds, and that frequency of errors was positively related to set size. Porter (1999) found that correspondence errors made by children with Down syndrome were more likely to result from skipping items than from double counting.
2) The count word sequence
During development, production of the count word sequence typically shows the following pattern. The first section of the produced sequence consists of part of the stable conventional sequence (e.g. one, two, three, four), this is followed by a stable non-conventional section (e.g. nine, twelve, seven), and then a non-stable portion in which the order and number words included change each time the child 'counts' (Fuson, Richards, & Briars, 1982). The stable conventional section progressively lengthens until the child can recite the standard sequence to 100 and beyond. A child producing stable but non-conventional count sequences can nevertheless be credited with understanding of the stable-order principle (Gelman & Gallistel, 1978).
Techniques to encourage children to produce a count word sequence in experimental settings include asking them to count as high as they can (Fuson, Richards, & Briars, 1982). To keep children on task, some sort of stimulus is useful; thus Baroody (1986) asked children to 'count' a set of stars with the experimenter maintaining one-one correspondence with the items.
If both the one-one and stable-order principles have been adhered to using a standard count word sequence, the final tag represents the cardinal value of the set. Even when children are able to count accurately, however, it does not follow that they realise that counting yields the cardinal value of a set.
3) Understanding of cardinality
Research with typically developing children shows understanding that the last count word indicates the numerosity of the whole set emerges 6 to 12 months after procedural counting skills have become established (Frye, Braisby, Lowe, Maroudas, & Nicholls, 1989; Wynn, 1990, 1992); in a UK population, cardinality was found to emerge a few months either side of the fourth birthday (Fluck & Henderson, 1996).
Evidence indicating understanding of cardinality includes emphasis or repetition of the final count word, either spontaneously or after the 'how many?' question (Gelman & Gallistel, 1978). However, use of this evidence has been criticised since such responses may have been learnt as a convention without any underlying understanding (Fuson & Hall, 1983; Frye et al., 1989 ; Wynn, 1990). An alternative test which is considered to be a more valid measure, is the give x task, where children are asked to give a specific number of items from a larger set (Schaeffer, Eggleston, & Scott, 1974). If they attempt to count out items this indicates that they understand the connection between counting and cardinality. In contrast, a child who simply grabs a handful of items to give, has not demonstrated such understanding. As no doubts exist over the validity of the give x task as a measure of understanding of cardinality it was chosen for the current study.
Social and cultural perspectives on number development
From the focus of previous research into number skills, which has mostly studied the child's skills in isolation, one might conclude that it is a purely internal, cognitive process. However, recent research has provided interest in the social aspects of the number domain. Durkin (1993) states that for children growing up in a culture where number is an established structure "...the main reason for worrying about how many there are of anything is that someone else wants to know" (p. 151). The input a child receives obviously affects factors such as the number words learnt, and these have been found to influence the child's development; e.g. Chinese has a decade pattern with a regular structure, unlike in English, giving Chinese students an advantage in the acquisition of arithmetical skills (e.g. Fuson & Kwon, 1991).
Less transparent is the effect social and cultural factors may have on the development of counting skills. Saxe, Guberman, and Gearhart (1987) investigated the role of parent-child interaction in number development and concluded that mothers adjusted the goal structure of the counting task to reflect their child's abilities. While this could be taken as evidence that the parent is scaffolding the child's learning, Durkin (1993) points out that the child may not have interpreted the interaction in the same way as the adult; thus mothers often assume that when their children count they understand cardinality, but this is not the case when the child first learns to count (Fluck, 1995).
Included in the recent interest in the development of number and counting skills and the influence of social interaction, has been the application of Vygotsky's (1978) theory of development (Fluck & Maltby, 1997; Linnell & Fluck, 2001). Development can be seen as an apprenticeship (Rogoff, 1990), with a more competent partner 'scaffolding' (Wood, Bruner & Ross, 1976) the child until they come to learn the "cognitive and communicative tools of their culture" (Tharp & Gallimore, 1991, p. 42). Counting is learnt as a joint social routine, whereby children learn the counting language of their particular culture. Skills gradually move from the interpersonal (social) level to the individual or psychological level (Vygotsky, 1978).
Vygotsky (1978) distinguished between what the child can achieve alone, what it can achieve with the help of an adult, and things that it cannot achieve even with help. The difference between what the child can do unaided and with support corresponds to the 'zone of proximal development'. It is suggested that this represents what the child is able to learn next - hence 'proximal development'. Measuring the zone of proximal development can provide a very different perspective on the child's ability to learn, compared to traditional IQ tests which measure 'static' ability (Brown & Ferrara, 1985). For example, where two children achieve the same on a particular task alone, they may well have very different levels of prospective development. In turn they will be able to take advantage of different levels of adult support. It is also important to note that a child will have a different zone of proximal development for each skill that is useful in their culture (e.g. counting, weaving, boat building), quite a different notion to the idea of giving a child a single static IQ score.
Fluck and Maltby (1997) concluded that there are individual differences in the support that parents of typically developing children provide when involved in number related interactions. They predict that these differences will be reflected in the readiness with which children develop cardinal understanding, and they are currently investigating this in a longitudinal study. We predict that this finding will be accentuated for children with Down syndrome. This approach is being used as a structure for studying individual differences in the development of number skills in children with Down syndrome, specifically the relationship between parent-child interaction and numerical development.
The current study investigates whether support from an adult significantly improves performance on the count task and whether the zone of proximal development model applies in the case of number skills in children with Down syndrome. While it may seem intuitively obvious that a child's performance will improve in situations where support is provided from their parent or other adult, this may not necessarily be the case, and if improvements are found one would wish to ask whether they are significant improvements. Vygotsky's theory would predict that children with learning disabilities would have smaller zones of proximal development, which means they make less of an improvement when given support than typically developing peers (Brown & Ferrara, 1985), and this will be tested in the current study with respect to counting tasks.
Method
Participants
These included 23 children with Down syndrome and 20 typically developing children selected on the basis of non-verbal mental age, together with their primary caregivers. In the Down syndrome group, 12 of the children were male and 11 female. Of the typically developing children, 13 were male and 7 female. The caregivers of the children with Down syndrome consisted of 20 mothers and 3 fathers. Of the typically developing children there were 19 mothers and 1 father. The children with Down syndrome were recruited through Down Syndrome Education International, covering the whole of the UK. The typically developing children were recruited through nurseries and parent and toddler groups in Hampshire.
Profile of the two groups
Chronological ages, non-verbal mental ages and language profiles of the two groups are shown in Table 1.
| Mean | SD | Min | Max | |
|---|---|---|---|---|
| DS (n=23) | ||||
| CA | 64.00 | 14.39 | 41.00 | 85.00 |
| Non-verbal MA (Leiter) | 39.83 | 6.19 | 29.00 | 48.00 |
| Language age* (n=19) | 21.32 | 4.44 | 13.00 | 29.00 |
| TD (n=20) | ||||
| CA | 36.70 | 6.93 | 24.00 | 48.00 |
| Non-verbal MA (Leiter) | 40.90 | 4.40 | 32.00 | 47.00 |
| Language age* (n=17) | 37.47 | 9.49 | 27.00 | 58.00 |
Children with Down syndrome:
Language measures could only be obtained for 19 of the 23 children with Down syndrome: The measures for those 19 children showed the following uneven cognitive profile: T-tests revealed that their language ages (M = 21.32 months) were significantly lower than their non-verbal mental age scores (M = 40.05 months), t (18) = 10.04, p < .001, which in turn were significantly lower than their chronological ages (M = 65.32 months), t (18) = -7.09, p < .001.
Typically developing children:
Language measures were obtainable for 17 of the 20 typically developing children: T-tests confirmed that their language skills (M = 37.47 months) were not significantly different from their chronological ages (M = 36.70 months), or non-verbal mental ages (M = 41.29 months). There was, however, a significant difference between these children's mean chronological (M = 36.00 months) and non-verbal mental ages (M = 41.29 months), t (16) = 4.04, p < .001.
Materials
Two fabric clown dolls (30 cm tall) and sets of small toys (cars, tins, packets, jigsaw pieces, animals, food) were used for the counting activities. Each set of toys to be counted was presented in a plastic basket, and an additional larger plastic basket was provided for the give x task.
Procedure
Assessments were carried out in either one or two visits, depending on distance the family had traveled to attend and on the child's level of attention. For all children, sessions started with a fifteen-minute free-play period, followed by the supported counting tasks and then the unsupported counting tasks.
The order of the supported and unsupported tasks was carefully considered. Gaining realistic and valid observations of parent-child interaction was felt to be the most important goal of the research, therefore parental support should not be influenced by parents observing the experimenter's presentation of the unsupported tasks immediately before taking part in the task themselves. In principle this design carries a risk of order effects, however this was the same for both groups of children. In addition, regular breaks and switching between tasks helped to dispel fatigue and boredom.
The standardised assessments were interspersed between the counting tasks, depending on the child's attention span and the perceived need to switch tasks. All procedures were conducted in a comfortable observation room with wall-mounted video cameras. Occasionally, one or both of the standardised assessments were carried out in the child's home as soon as could be arranged after completion of the counting tasks. The gap between these testing sessions was never more than one week.
Number sequence task
This task, used successfully in a previous study of children with Down syndrome (Nye, Clibbens, & Bird, 1995), was designed to elicit count words without imposing the additional burden of counting a set of items (Baroody, 1986). The child was presented with a card containing 40 stars and the experimenter asked, "Can you count as high as you can for Charlie (clown doll)? You count while Charlie points to the stars." The count was stopped if the child was obviously uncomfortable about continuing, began to repeat previously used segments, or had exhausted his/her standard sequence.
A full transcript was made of the number words spoken by each child. Only sequences produced in unsupported conditions are reported here, including data from the unsupported count and give x tasks as well as the 'Star Card' task. Two sets of measures were employed:
1) Highest count sequence (HCS)
One point is allocated for each number heard as part of a correctly produced conventional sequence starting from '1', e.g. "1, 2, 3, 4, 5" equates to a score of 5.
2) Total number of number words observed (TNW)
One point is allocated for each different number name produced, whether part of a sequence or not; e.g. "I got 5 cars!" This second measure is used to explore the whole of the children's number vocabulary, and allows credit to be given to children whose count sequences include non-conventional stable sections. It also gives credit for knowledge of 'outliers', i.e. number words known by a child, but not necessarily used as part of a stable count sequence.
Structured counting activities
Each child performed two counting tasks involving a clown doll and his baskets of toys (adapted from Linnell, 1998; Linnell & Fluck, 2001). Count task - the child was asked to count a set of loose objects for the clown as 'he is not very good at counting and he needs some help'. Give x task - the child was asked to give the clown a specific number of items. Each of these tasks was performed in two different conditions, supported and unsupported. In the supported condition, parents were asked to give their children any help they needed to succeed on the task. In the unsupported condition a female experimenter administered the task, encouraging the child, but not providing any support beyond that. Different clown dolls were used for the supported and unsupported conditions, to give the child a reason for carrying out the task again.
Six trials were completed for each task in both conditions, one for each of the set sizes 2, 3, 5, 7, 10, and 18, using a range of toys. Set size and item type were counterbalanced across presentations according to a Latin square design.
Scoring criteria for the count task
In order to succeed in counting a set of items the child must not only produce the correct count sequence in the right order but also maintain one-one correspondence between the count words and the items. The score allocated was the largest set size the child was able to count in accordance with these criteria. In the supported condition, to be deemed successful on a trial, the child had to supply the last count word correctly without imitating.
Calculation of the zone of proximal development for procedural counting
The child's zone of proximal development for procedural counting was calculated as the difference between the unsupported and supported count scores (supported minus unsupported).
Scoring criteria for the give x task
Performance on the give x task can be investigated in two ways. The first is the maximum number of items that the child can give accurately; the child can be given a score equal to this number. According to this criterion, successful performance requires the ability to count accurately, to remember the requested amount while counting, and to be able to stop when that amount has been reached.
The second, and more interesting for the investigation of conceptual understanding, is the strategy employed by the child. In previous studies (Wynn, 1990; Fluck & Henderson, 1996) children have been found either to grab handfuls of items to give ('grab') or to attempt to count out the requested amount ('count'). A 'count' response implies that the child appreciates the cardinal significance of counting, even if that response itself is inaccurate. Children were classified as 'counters' if they demonstrated any counting during the give x task, and as 'grabbers' if they did not.
Standardised assessments
Non-verbal general ability was measured using the Leiter International Performance Scale (Leiter, 1979).
To measure productive language ability, children who were not fatigued after having completed all other assessments were assessed using the Reynell Developmental Language Scales (Reynell & Huntley, 1987). If the child was unable to complete this assessment then parents were asked to complete the MacArthur Communicative Development Inventories ( Fenson, et al., 1993 ). In effect this meant that at Phase 1 the majority of children with Down syndrome were assessed using the MacArthur and the majority of typically developing children assessed using the Reynell. Each of these scales can be converted into an age equivalent score and will be referred to as the child's 'language age'.
Results
Since inspection of histograms revealed that distribution of the data was skewed, non-parametric tests were used for all analyzes.
Count Word Production
It was predicted that children with Down syndrome would produce shorter conventional count sequences and fewer different count words than their typically developing counterparts.
Unsupported production of the conventional count sequence: Highest count sequence
Table 2 shows the highest count sequence scores for each group. A Mann-Whitney test confirmed that the Down syndrome group produced significantly shorter count sequences, U (23, 20) = 99, p =.0005, one-tailed.
| n | Median | Inter-quartile range | Min | Max | |
|---|---|---|---|---|---|
| DS group | 23 | 3 | 6 | 0 | 19 |
| TD group | 20 | 11 | 8.25 | 0 | 15 |
The distribution of count scores is shown in Figure 1, where it will be noted that for the Down syndrome group, the range of scores was between 0 and 19, with 8 of the 23 children scoring 0, and the majority (14 children) scoring between 1 and 8. In contrast the distribution for the typically developing children shows one cluster of scores up to 5, and a second cluster between 9 and 15.
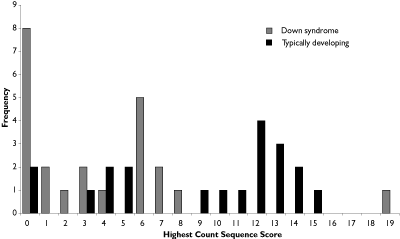
Figure 1. Distribution of Highest Count Sequence scores (Down syndrome and typically developing groups).
A boxplot produced by SPSS identified the score of 19 in the Down syndrome group as an extreme outlier, therefore the analysis was re-run with this individual removed. This Mann-Whitney test confirmed that the Down syndrome group produced significantly shorter count sequences, U (22, 20) = 112.5, p =.0025, one-tailed. It should be noted that the median Highest Count Sequence score for the Down syndrome group was now 2.
Unsupported total count word vocabulary: Total number of count words
Table 3 shows the median and range of scores, and Figure 2 represents the distribution of the data for both groups. A Mann-Whitney test revealed that the typically developing group had a significantly higher total vocabulary than the Down syndrome group U (23, 20) = 116, p =.0025, one-tailed. A greater proportion of children with Down syndrome (35%) did not produce any count words during the unsupported tasks, compared to the typically developing group (10%).
| n | Median | Inter-quartile range | Min | Max | |
|---|---|---|---|---|---|
| DS group | 23 | 3 | 11 | 0 | 22 |
| TD group | 20 | 13 | 10.5 | 0 | 19 |
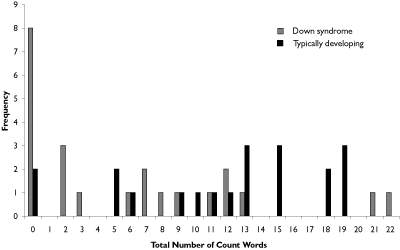
Figure 2. Distribution of Total Number Word Count scores (Down syndrome and typically developing groups).
Comparing the medians in Tables 2 and 3, it can be seen that the typically developing children produce more individual count words than they could recite in a sequence, and this difference was found to be highly significant using a Wilcoxon test (z = -3.194, p = .0005, one-tailed).
Although for the Down syndrome group there does not appear to be a difference between the two sets of scores from inspection of the median scores (median = 3 for both HCS and TNW), a Wilcoxon signed ranks test indicates that there is indeed a significant difference between them (z = -2.814, p = .0025, one-tailed). This difference remained when the data was tested with the outlier in the Highest Count Sequence data removed (z = -2.673, p = .004, one-tailed).
Procedural Counting of Objects
Unsupported performance
The score allocated to each child is the largest set size they are able to count according to the criteria described in the Procedure. Inspection of the median scores (Table 4) indicates that the typically developing children were able to count significantly larger sets than those with Down syndrome, in the unsupported condition. A Mann-Whitney test revealed that the two groups differed significantly in their count scores U (23, 20) = 131.5, p =.007, one-tailed. An outlier was identified in the Down syndrome group and the analysis re-run. The significant difference between groups remained, U (22, 20) = 112.5, p =.0025, one-tailed.
| Task | Group | n | Median | Inter-quartile range | Min | Max |
|---|---|---|---|---|---|---|
| Unsupported performance | DS group | 23 | 2 | 3 | 0 | 10 |
| TD group | 20 | 4 | 5 | 0 | 10 | |
| Supported performance | DS group | 23 | 7 | 8 | 0 | 18 |
| TD group | 20 | 10 | 8 | 0 | 18 |
Supported performance
The median scores shown in Table 4 indicate that the performance of each group increased in the supported condition. Wilcoxon signed ranks tests performed separately for each group confirmed that there was a significant difference between unsupported and supported object counting scores in both cases (Down syndrome group [outlier removed]: z =-3.413, p =.0005; typically developing group: z =-3.627, p =.001). This is clearly illustrated in Figure 3 and Figure 4, though it can also be seen that some children in both groups did not improve their performance in the supported condition.
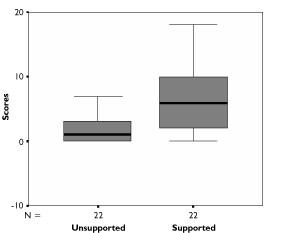
Figure 3. Distribution of unsupported and supported count scores (Down syndrome group).
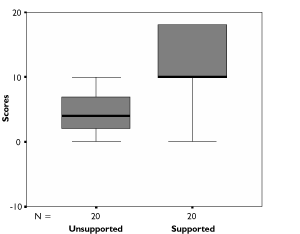
Figure 4. Distribution of unsupported and supported count scores (typically developing group).
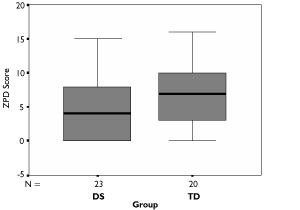
Figure 5. Distribution of zone of proximal development scores for object counting (DS and TD groups).
Zone of proximal development for procedural counting
As described earlier, the zone of proximal development for procedural counting measure in the current study is the difference between the child's supported and unsupported maximum count scores. It was predicted that children with Down syndrome would have significantly smaller zones of proximal development for counting than typically developing children. Table 5 shows the median and range of scores for each group. A Mann-Whitney test showed that the size of the increase in performance with parental support did not differ significantly between the two groups, U (23, 20) = 169.5, n.s. Therefore, the hypothesis that children with Down syndrome would have smaller zones of proximal development for object counting than typically developing children was not supported.
| Group | n | Median | Inter-quartile range | Min | Max |
|---|---|---|---|---|---|
| DS group | 23 | 4 | 8 | 0 | 15 |
| TD group | 20 | 7 | 7 | 0 | 16 |
Does count sequence production restrict object counting?
Though the current study does not make a detailed examination of counting errors and how they may be restricting the children's ability to count items, it can be asked whether the children's production of the count word sequence is restricting success on the unsupported count task. The highest count sequence scores (outlier removed) and the maximum count scores in the unsupported condition (see Table 6) were found to differ significantly for both the Down syndrome and typically developing groups, using Wilcoxon tests (Down syndrome group: z = -2.68, p = .007; Typically developing group: z = -3.577, p = .001). Inspection of the median scores shows that the children could produce significantly longer sequences than they could successfully use in the count task. Thus, object counting was not restricted by limited sequence knowledge for either group.
| Group | Task | n | Median | Inter-quartile range | Min | Max |
|---|---|---|---|---|---|---|
| DS group | Highest count sequence | 22 | 2.5 | 6.0 | 0 | 8 |
| Object counting | 22 | 1.0 | 3.0 | 0 | 7 | |
| TD group | Highest count sequence | 20 | 11.5 | 8.8 | 0 | 15 |
| Object counting | 20 | 4.0 | 5.0 | 0 | 10 |
Understanding of Cardinality: The Give X Task
It was predicted that neither group of children would display an understanding of cardinality in this first phase of the longitudinal study. Only two of the typically developing children were aged four years, which is the age at which Fluck and Henderson (1996) found children to demonstrate understanding of cardinality. Of the children with Down syndrome, 20 out of 23 had a chronological age of 47 months or above, but only three had a non-verbal mental age above this level.
It should be noted that 7 out of the 23 children with Down syndrome were not tested on the unsupported give x task, either because they refused to take part or because they were already fatigued and not performing well on previous tasks.
Giving accurate set sizes
The first way of looking at performance on the give x task is to see how many items a child can give accurately. Table 7 shows the number of children in each group who were able to give each set size requested. The majority of children in both groups were unable to give any of the set sizes accurately. Only 2 of the 14 children with Down syndrome and 7 of the 20 typically developing group were able to give small, subitizable sets. No child in either group could accurately give more than 3 items. Thus, none of the children in Phase 1 of the study demonstrated understanding of cardinality according to this criterion.
| DS group | TD group | |
|---|---|---|
| Fail | 14 | 13 |
| Success* | 2 | 7 |
| Total number tested | 16 | 20 |
A chi-square test revealed no significant difference between the proportion of children who succeeded and failed in each of the two groups, c 2 (1, N = 36) = 2.4, p = .121. Hence there is no significant difference between the groups in the current sample with respect to their level of accuracy in giving sets of items.
While performance on the give x task measured by this criterion provides some information about understanding of cardinality, success is partly dependent on the ability to count accurately, remember the amount requested, and stop when the correct amount has been reached. The alternative criterion is the strategy chosen by the child, irrespective of how accurately it is used.
Strategies observed on give x task
It was predicted that no counters would be seen in this phase, again based on the finding that most children do not demonstrate understanding of cardinality before four years of age (Fluck & Henderson, 1996). Table 8 shows the number of counters and grabbers observed in each group. Unexpectedly, some counters were found in each group.
| Group | Grabbers | Counters | Total number of children tested |
|---|---|---|---|
| DS group | 10 | 6 | 16 |
| TD group | 13 | 7 | 20 |
A chi-square test revealed no significant difference between the proportion of counters and grabbers in the two groups, c 2 2 (1, N = 36) = .024, n.s. Hence there is no significant difference between the groups in the current sample with respect to their understanding of cardinality.
Discussion and conclusion
The results show significant differences between the children with Down syndrome and typically developing children in procedural counting skills, more specifically in production of the count sequence and object counting. On both of these measures the typically developing children performed significantly better than those with Down syndrome, matched on non-verbal ability. Support from an adult was found to improve performance on the count task significantly for both groups of children, and there was no significant difference between the groups in the degree of improvement shown, i.e. zone of proximal development. No significant differences were found between the two groups on assessments of cardinal understanding.
As expected, differences were found between the children with Down syndrome and typically developing children on productive number vocabulary, both for the conventional count sequence and total count word vocabulary. Consistent with previous research on acquisition of the count word sequence (Fuson, 1988), however, the children in both groups produced more individual count words than they were able to recite in a sequence. The mean language age of the children with Down syndrome was significantly below their mean non-verbal mental age and mean chronological age, whereas the typically developing children had a relatively consistent profile on these three measures. As the children were matched on non-verbal mental age it is not surprising that a difference has been found on the language component of the number skills assessed here.
The typically developing children were able to count significantly larger sets of objects. For both groups, object counting was not restricted by limited count sequences. Nevertheless, the children with Down syndrome counted fewer objects than their typically developing peers, therefore further investigation of individual performance is required.
Support from an adult was found to significantly improve performance on the count task for both groups of children. The increase in performance with support was not significantly different between the two groups, indicating that the children with Down syndrome are benefiting as much from support as the typically developing children, contrary to our original predictions. If the difference between the supported and unsupported condition is taken as a measure of the child's zone of proximal development, for the groups studied here there does not seem to be a difference between the mean zone of proximal development for the Down syndrome and typically developing groups.
Arguably, measuring the zone of proximal development in this way should really be taken as a measure of the performance of the dyad in working together, rather than as a measure of the child's potential for development, as we cannot be sure that parent-child interaction is operating at an optimum level to ensure the child's success. Alternative methods of measuring a child's zone of proximal development have been used where a structured scale of prompts allows measurement of the amount of support the child needs to succeed on a task compared to performance alone (e.g. Rutland & Campbell, 1996). The measure of zone of proximal development adopted in the current study assumes that parents are giving optimal support to their child, but further analysis is required to identify the strategies that parents are using to support their child and how far these are successful. The type of support given can be expected to have an impact on the child's development (Fluck & Maltby, 1997). The current sample is being followed longitudinally with the aim of identifying the influence of parental support on the children's development of counting and understanding of cardinality over the following year, for both typically developing children and children with Down syndrome.
The children with Down syndrome studied in this sample show a similar pattern of response in the assessment of cardinal understanding compared with the typically developing group. It was first of all surprising that any of the children would demonstrate understanding of cardinality as Fluck and Henderson (1996) found that children did not demonstrate this understanding until round their fourth birthday, although Wynn (1990, 1992) found that an American sample passed the give x task at only 3 years 6 months. Probably more interesting than establishing age milestones is investigation of the emergence of understanding of cardinality in relation to procedural counting skills, and this will be carried out in analyzes of later phases of the longitudinal study.
Since the groups were matched on non-verbal mental age, it was predicted that the results would be in line with those of Gelman and Cohen (1988), as they also used a general ability measure to match the children. Gelman and Cohen found a difference between the children with Down syndrome and typically developing children on the counting tasks, and this was supported in the current study with respect to procedural counting skills. However, the current results for understanding of cardinality are more similar to those of Caycho et al. (1991), with no difference between the two groups, despite the fact that Caycho et al. matched their children on receptive language skills.
It is possible that a 'floor' effect has occurred, whereby the typically developing children were generally not yet at a point where they would be expected to pass the give x task (i.e. before age 3 years 6 months). Indeed it is even more surprising that so many of the children with Down syndrome passed the give x task. Therefore the fact that there is no difference between the groups may be an artefact of the data. It will be interesting to see how development progresses in the longitudinal study.
An alternative possibility is that the current cohort of children with Down syndrome has benefited from improvements in experiences of counting and number activities presented in their social and educational environment. Expectations that children with Down syndrome will achieve more are increasing with each generation, and the current sample of children have all benefited from receiving intensive early intervention programs. All were either attending or due to attend their local mainstream school, which has been found to have a significant effect on numerical skills ( Sloper et al., 1990 ).
While matching on the basis of non-verbal ability allows us to draw certain conclusions about the development of numerical skills in children with Down syndrome in comparison to typical development, at present the two groups are significantly different in several ways - the profile of language difficulties usually displayed by children with Down syndrome means that we are unable to match for chronological age, language and non-verbal age with one set of typically developing children. For this reason the longitudinal data will be investigated using groups of children matched on different criteria to perform analyzes. One solution will be to match on the basis of language ability or one aspect of numerical ability (e.g. Porter, 1999), matching children from across phases of the longitudinal study if necessary, and compare the profile and development of other skills. In addition, whether the similarity between the two groups remains as the children develop over time will be revealed as the longitudinal data is examined.
The children with Down syndrome in the current study produced significantly fewer count words, shorter count sequences and the largest set of items they are able to count is significantly smaller than the typically developing group they have been matched with. In contrast, the groups performed equally well on the test assessing understanding of cardinality, and over a third of children in each group were unexpectedly classified as having understanding of cardinality. This profile would seem to be the complete reverse of the standard picture presented of number skills in children with Down syndrome, whereby they are seen to have rote procedural skills but no conceptual understanding. The current analysis looks at the children's performance on the tasks at quite a gross level and there is much subtle variation requiring further investigation. In addition, results from the longitudinal study of both groups of children will provide far more valuable information about development than the current cross-sectional data.
Acknowledgements
The research was supported by a bursary from the University of Portsmouth to the first author, and testing facilities were provided by the Down Syndrome Educational Trust. The authors would like to thank the families who took part in the project, and Dr. Maggie Linnell for discussions concerning counting tasks. This paper is based on a presentation made by the first author at the Fourth European Down Syndrome Conference, Malta (10-13 March 1999).
Correspondence
Joanna Nye • Department of Psychology, University of Portsmouth, King Henry Building, King Henry I Street, Portsmouth, PO1 2DY. • E-mail: joanna.nye@port.ac.uk
References
- Antell, S. E., & Keating, D. P. (1983). Perception of numerical invariance in neonates. Child Development, 54, 695-701.
- Baroody, A. J. (1986). Counting ability of moderately and mildly handicapped children . Education and Training of the Mentally Retarded, 21, 289-300.
- Brown, A. L., & Ferrara, R. A. (1985). Diagnosing zones of proximal development. In J. V. Wertsch (Ed. .), Culture, Communication and Cognition: Vygotskian Perspectives (pp. 273-305). Cambridge: Cambridge University Press.
- Buckley, S. (1985). Attaining basic educational skills: reading, writing and number. In D. Lane, & B. Stratford (Eds.), Current Approaches to Down Syndrome (pp. 315-343). London: Holt, Rinehart and Winston.
- Byrne, A. (1997). The development of reading skills in children with Down syndrome. Unpublished doctoral dissertation, University of Portsmouth, Portsmouth, UK.
- Carr, J. (1988). Six weeks to twenty-one years old: A longitudinal study of children with Down's syndrome and their families. Journal of Child Psychology and Psychiatry, 29(4), 407-431.
- Caycho, L., Gunn, P., & Siegal, M. (1991). Counting by children with Down syndrome. American Journal on Mental Retardation, 95(5), 575-583.
- Chi, M. T. H., & Klahr, D. (1975). Span and rate of apprehension in children and adults . Journal of Experimental Child Psychology, 19, 434-439.
- de Graaf, E., & de Graaf-Posthumus, M. (1997, October ) . Learning elementary maths: Case study of a Dutch boy. Paper presented at Sixth World Congress on Down Syndrome, Madrid, Spain.
- Durkin, K. (1993). The representation of number in infancy and early childhood. In C. Pratt, & A. F. Garton (Eds.), Systems of Representation in Children (pp. 133-166). Chichester: John Wiley and Sons Ltd.
- Fenson, L., Dale, J., Resnick, S., Thal, D., Bates, E., Hartung, J. P., Pethick, S., & Reilly, J. S. (1993) . MacArthur Communicative Development Inventories: User's Guide and Technical Manual. San Diego, CA: Singular Publishing Group, Inc.
- Fluck, M., & Henderson, L. (1996). Counting and cardinality in English nursery pupils. British Journal of Educational Psychology, 66, 501-517.
- Fluck, M., & Maltby, M. (1997, June). Social factors in early number development. Paper presented at the 27th Symposium of the Jean Piaget Society, Santa Monica, CA .
- Fluck, M. J. (1995). Counting on the right number: Maternal support for the development of cardinality. The Irish Journal of Psychology, 16(2), 133-149.
- Frye, D., Braisby, N., Lowe, J., Maroudas, C., & Nicholls, J. (1989). Young children's understanding of counting and cardinality. Child Development, 60, 1158-1171.
- Fuson, K. C. (1988). Children's Counting and Concepts of Number. New York: Springer-Verlag.
- Fuson, K. C., & Hall, J. W. (1983). The acquisition of early number word meanings: A conceptual analysis and review. In H. Ginsburg (Editor), The Development of Mathematical Thinking. (pp. 49-107) New York: Academic Press.
- Fuson, K. C., & Kwon, Y. (1992). Korean children's single-digit addition and subtraction: Numbers structured by ten . Journal for Research in Mathematics Education, 23(2), 148-165.
- Fuson, K. C., Richards, J., & Briars, D. J. (1982). The acquisition and elaboration of the number word sequence. In C. J. Brainerd (Ed.), Children's Logical and Mathematical cognition: Progress in Cognitive Developmental Research (pp. 33-92). New York: Springer-Verlag.
- Gelman, R., & Cohen, M. (1988). Qualitative differences in the way Down syndrome and normal children solve a novel counting problem. In L. Nadel (Ed.), The Psychobiology of Down's Syndrome (pp. 51-99). Cambridge, MA: MIT Press.
- Gelman, R., & Gallistel, C. R. (1978). The Child's Understanding of Number. Cambridge, MA: Harvard University Press.
- Leiter, R. G. (1979) . Leiter International Performance Scale (Revised): Instruction Manual. Wood Dale, IL: Stoelting.
- Linnell, M.E. (1998) The influence of social interaction on the development of cardinality in pre-school children. Unpublished doctoral dissertation. University of Portsmouth, Portsmouth, UK.
- Linnell, M.E. & Fluck, M. (2001) The effect of maternal support for counting and cardinal understanding in pre-school children. Social Development, 10 (2), 202-220.
- Monari Martinez, E. (1999, October). Learning and mathematics at school and .... later on. Paper presented at The Joy of Living: International Down Syndrome Conference, Jerusalem, Israel.
- Monari Martinez, E. (1998). Teenagers with Down syndrome study algebra in high school. Down Syndrome Research and Practice, 5(1), 34-38. [Read Online]
- Paterson, S. J. (2001) Language and number in Down syndrome: The complex trajectory from infancy to adulthood. Down Syndrome Research and Practice, 7(2), 83-90. [Read Online]
- Paterson, S. J., Brown, J. H., Gsödl, M. K., Johnson, M. H., & Karmiloff-Smith, A. (1999) . Cognitive modularity and genetic disorders. Science, 286, 2355-2358.
- Porter, J. (1999). Learning to count: A difficult task? Down Syndrome Research and Practice, 6(2), 85-94. [Read Online]
- Reynell, J., & Huntley, M. (1987). Reynell Developmental Language Scales Manual: 1987 Edition. Windsor: NFER-Nelson.
- Rogoff, B. (1990). Apprenticeship in Thinking: Cognitive Development in Social Context. New York: Oxford University Press.
- Rutland, A. F., & Campbell, R. N. (1996). The relevance of Vygotsky's theory of the 'zone of proximal development' to the assessment of children with intellectual disabilities. Journal of Intellectual Disability Research, 40(2), 151-158.
- Saxe, G. B., Guberman, S. R., & Gearhart., M. (1987). Social processes in early number development . Monographs for the Society for Research in Child Development, 52(2, Serial no. 216).
- Schaeffer, B., Eggleston, V. H., & Scott, J. L. (1974). Number development in young children. Cognitive Psychology, 6, 357-379.
- Siegler, R., & Shipley, C. (1987). The role of learning in children's strategy choices. In L. S. Liben (Ed.), Development and Learning: Conflict and Congruence? (71-107) Hillsdale, NJ: Lawrence Erlbaum Associates.
- Sloper, P., Cunningham, C., Turner, S., & Knussen, C. (1990). Factors relating to the academic attainments of children with Down's syndrome. British Journal of Educational Psychology, 60, 284-298.
- Starkey, P., & Cooper, R. G. (1995). The development of subitizing in young children. British Journal of Developmental Psychology, 13, 399-420.
- Starkey, P., Spelke, E., & Gelman, R. (1990). Numerical abstraction by human infants. Cognition, 36, 97-127.
- Tharp, R., & Gallimore, R. (1991). A theory of teaching as assisted performance. In P. Light, S. Sheldon & M. Woodhead (Eds.), Learning to Think. London: Routledge & The Open University.
- Vygotsky, L. (1978). Mind in Society: The Development of Higher Mental Processes. Cambridge, MA: Harvard University Press.
- Wagner, S. H., & Walters, J. (1982). A longitudinal analysis of early number concepts: From numbers to number. In G. E. Foreman (Ed.), Action and Thought: From Sensorimotor Schemes to Symbolic Operations (pp. 137-161). London: Academic Press.
- Wood, D. J., Bruner, J. S., & Ross, G. (1976). The role of tutoring in problem solving. Journal of Child Psychology and Psychiatry, 17(2), 89-100.
- Wynn, K. (1990). Children's understanding of counting . Cognition, 36(2), 155-193.
- Wynn, K. (1992). Children's acquisition of the number words and the counting system. Cognitive Psychology, 24, 220-251.

